Example proofs and non-proofs

With quantifiers, functions, and equality, we have a greater richness of expression. Since each of the symbols mimics standard rhetorical techniques, we still recognize some common patterns as encapsulated via provable formula.

Order of quantifiers

Can we prove \(\forall y~ \exists x~ A(x,y) \to \exists x~ \forall y~ A(x,y)\) in general?

To approach this, it makes sense to try to find a simple model and figure if the statement is true. Let’s take $\mathbb{N}$ and interpret $A(x,y)$ as $x=y$. Then, in natural language, the head of the implication says that for any number $y$ there is some other number $x$ such that $x=y$. This of course is always true! We can take our desired $y$ to be $x$.

The tail of the implication says that there is a single number $x$ such that for every number $y$ we have $x=y$. This is clearly false as not all numbers are equal.

Thus, this formula cannot be proven. We cannot exchange quantifiers thoughtlessly.

Is the other direction provable? Our initution from the particular in encouraging and in fact it is.

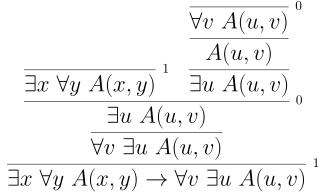
We use new variable labels to make things clear. The intuition of the proof here says that we can the witness of the first existential quantifier as the witness of the second.

We can freely exchange the same quantifiers. Below is a proof of $ \forall x~ \forall y~ A(x,y) \vdash \forall y~ \forall x~ A(x,y)$.

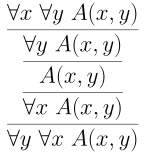
Similiarly, we can exchange existential quantifiers.

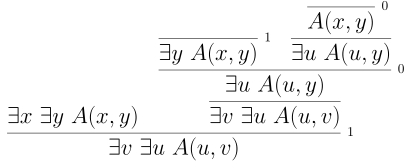
Given this we often write $\forall x~ y$ in place of $\forall x~ \forall y~$ and $\exists x~ y$ for $\exists x~ \exists y$ to shorten notation.

Negation and quantifiers

We have seen how to exchange $\neg$ and other connectives like $\land$ and $\lor$.

Let’s try to understand $\neg (\exists x~ A(x))$. This is saying no matter what the value of $x$ is $A(x)$ should not be true. That looks much like $\forall x~ \neg A(x)$. This also comports with our analogy between $\forall$ and $\land$ and $\exists$ and $\lor$. Let’s try to give a proof.

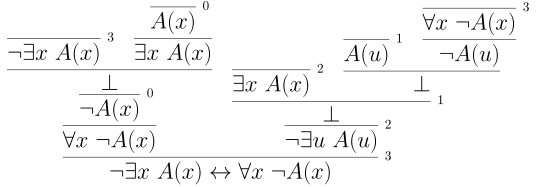
Similarly, $\neg \forall x~ A(x) \leftrightarrow \exists x~ \neg A(x)$ is a valid formula. In fact, we have already been using this logical pattern in our arguments. It is usually called finding a counter-example. The counter-example being the witness to $\exists x~ \neg A(x)$.

Quantifiers and con/disjunction

From our analogy between $\forall$ and $\land$ and $\exists$ and $\lor$, we can guess at the behavior when quantifiers and con/disjunction interact.

Indeed, the following are valid formula. \(\forall x~ (A(x) \land B(x)) \leftrightarrow \forall x~ A(x) \land \forall x~ B(x) \\ \exists x~ (A(x) \lor B(x)) \leftrightarrow \exists x~ A(x) \lor \exists x~ B(x)\)

Let’s think about $\forall x~ (A(x) \lor B(x))$ vs $\forall x~ A(x) \lor \forall x~ B(x)$. Inituitively, whether $A(x)$ or $B(x)$ is true might depend on $x$. For example, in the model $\mathbb{N}$ where we interpret $A(x)$ as $x$ is even and $B(x)$ as $x$ is odd. Then, we know that everyone number is either even or odd. But not every number is even. Neither is every number odd.

There is a still an implication.

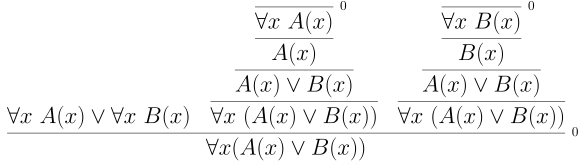
Similarly, one direction of distrubition of $\exists$ over $\land$ is valid.

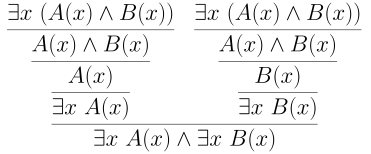
But if we use the model $\mathbb{N}$ with $A(x)$ being $x > 2$ and $B(x)$ being $x < 1$. Then $\exists x~ A(x) \land \exists x~ B(x)$ is true as there are numbers greater than $2$ and there are also numbers less than $1$ (namely $0$). However, $\exists x~ (A(x) \land B(x))$ is not true since no number is both less than $1$ and greater than $2$.

Unique existence \(~\exists !\)

Often, in mathematics, we are concerned with whether a list of conditions can completely specify something, be it a number, a formula, or something else. This pattern of logic is common enough that we introduce some shorthand notation.

The formula \(\exists x~ (A(x) \land \forall y~ (A(y) \to (x=y)))\) says that there is some $x$ that makes $A(x)$ true and if there is any other value that makes $A(x)$ true then in fact it had to be the original value.

This formula get its own compact notation: $\exists ! x~ A(x)$. This is read as there exists a unique $x$ satisifying $A(x)$.