Proof by contradiction

Suppose I can establish an absurdity by assuming the negation of something. What does this give us? Well, given $\neg A \vdash \bot$, we can prove $\neg \neg A$.

If we that the sun is not not up, that usually means that it is actually up, right?

More formally, we want to know about jutisfying \(\neg \neg A \vdash A\) Can this be done using the rules so far?

Unfortunately, nothing in our rules so far will allow us establish this. Adding this rule to our existing system yields some very useful conclusions.

For example, given $\neg A \vdash \bot$, we already knew we could establish $\vdash \neg \neg A$ but now we also have $\vdash A$.

The process of establishing $A$ by assuming $A$ doesn’t hold and arguing to a contradiction goes by the Reductio ad absurdum (RAA) or proof by contradiction.

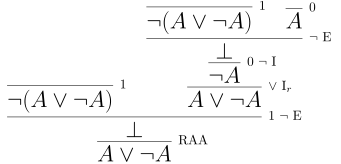
Another well-known conclusion is the Law of the Excluded Middle which is just \(A \lor \neg A\) In other words, no matter what $A$ is either $A$ holds or it is doesn’t.

You might take a moment and think this an immutable law of reality. Our day-to-day experience definitely leads us to think this. But reality in general is more complicated. Think of Schrodinger’s cat. Is the cat alive or not alive in the box? What is the state of the unobserved wave function?

But in an idealized world proof by contradiction is a perfectly reasonable assumption. And mathematicians, for the most part, tend to idealize our world.

Below is a proof the Law of Excluded Middle using proof by contradiction.

Given an formula of the form $A \to B$, the contrapositive is the formula \(\neg B \to \neg A\)

Let’s justify \(A \to B \vdash \neg B \to \neg A\)

Below is a natural deduction proof

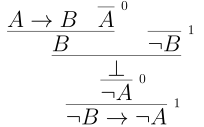
If we substitute $\neg B$ for $A$ and $\neg A$ for $B$, we immediately have \(\neg B \to \neg A \vdash (\neg \neg A) \to (\neg \neg B)\) With proof by contradiction, we get \(\neg B \to \neg A \vdash A \to B\)

Establishing the contrapositive and deducing the original statement is uncommonly common pattern in mathematical argument.