Making new sets from old

The empty set. A special role is played by the set with no elements. The empty set, denote $\varnothing$, satisfies \(\forall x~ x \not \in \varnothing\)

It enjoys nice properties with respect to unions and intersections: \(X \cup \varnothing = X \\ X \cap \varnothing = \varnothing\)

Unions. Given two sets $X$ and $Y$ we can make a new one whose elements are those which come from $X$ or from $Y$ \(X \cup Y := \lbrace z \mid z \in X \text{ or } z \in Y \rbrace\)

For example, if $X = \lbrace 0,2,4\rbrace$ and $Y = \lbrace 0,1,3\rbrace$ then \(X \cup Y = \{0,1,2,3,4\}\)

Note that $X,Y \subseteq X \cup Y$.

Intersections. We can instead ask for the elements that are in both $X$ and $Y$. \(X \cap Y := \lbrace z \mid z \in X \text{ and } z \in Y \rbrace\)

For example, if $X = \lbrace 0,2,4\rbrace$ and $Y = \lbrace 0,1,3\rbrace$ then \(X \cap Y = \{0\}\)

Note that $X \cap Y \subseteq X,Y$.

Complements. Another sensible thing to ask is that $z \in X$ but $z \not \in Y$ or vice versa. \(X \setminus Y := \lbrace z \in X \mid z \not \in Y \rbrace\)

For example, if $X = \lbrace 0,2,4\rbrace$ and $Y = \lbrace 0,1,3\rbrace$ then \(X \setminus Y = \{2,4\}\)

A special case is when $X = \mathcal U$. Then we write \(X^c := \mathcal U \setminus X\) Note that $X \setminus Y \subseteq X$.

Unions, intersections, and complements can be understood with Venn diagrams.

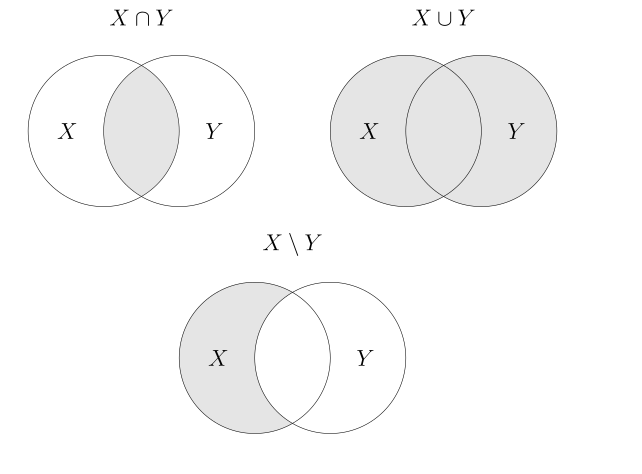
Products. The Cartesian product of sets $X$ and $Y$, denote $X \times Y$ is \(X \times Y := \lbrace (x,y) \mid x \in X \text{ and } y \in Y \rbrace\) Its elements consists of ordered pairs $(x,y)$ whose first entry is an element of $X$ and whose second is an element of $Y$. Two ordered pairs $(x_1,y_1)$ and $(x_2,y_2)$ are equal if and only if their components are equal $x_1=x_2$ and $y_1=y_2$.

For example, if $X = \lbrace 0,2,4\rbrace$ and $Y = \lbrace 0,1,3\rbrace$ then \(X \times Y = \{(0,0),(0,1),(0,3),(2,0),(2,1),(2,3),(4,0),(4,1),(4,3)\}\)

We often use a line to represent $\mathbb{R}$. The plane represents $\mathbb{R}^2 = \mathbb{R} \times \mathbb{R}$.

Power sets. Given a set $X$ we can form the set whose elements are all subsets of $X$. This called the power set of $X$ and is denoted by $\mathcal P(X)$.

For example if $X = \lbrace 0,2,4 \rbrace$, then \(\mathcal P(X) = \lbrace \varnothing, \lbrace 0 \rbrace, \lbrace 2 \rbrace, \lbrace 4 \rbrace, \lbrace 0,2 \rbrace, \lbrace 0,4 \rbrace, \lbrace 2,4 \rbrace, \lbrace 0,2,4 \rbrace \rbrace\)

Families of sets. Unions, intersections, and products are binary operations on sets: they take two sets and make new one.

We can upgrade these a bit. A family of sets is a set of sets indexed by a set. We used set a lot there. More precisely, we have a indexing set $I$ and for each element $i \in I$, we have a set $X_i$. Then \(\bigcup_{i \in I} X_i := \lbrace x \mid x \in X_i \text{ for some } i \in I \rbrace \\ \bigcap_{i \in I} X_i := \lbrace x \mid x \in X_i \text{ for all } i \in I \rbrace\)

We can also for the infinite product $\prod_{i \in I} X_i$ whose elements are functions $f : I \to \mathcal U$ with $f(i) \in X_i$ for each $i$.

For example, let’s take $X_n = [0,1/(n+1)) \subset \mathbb{R}$ where $n \in \mathbb{N}$ is our indexing set. Then, \(\bigcup_{n \in \mathbb{N}} X_n = [0,1) \\ \bigcap_{n \in \mathbb{N}} X_n = \lbrace 0 \rbrace\) One can understand $\prod_{n \in \mathbb{N}} [0,1/(n+1))$ as half-infinite sequences of real numbers \(x_0,x_1,x_2,x_3,\ldots,x_m,\ldots\) where $0 \leq x_n < 1/(n+1)$.

Identities

These operations satisfy many identities relating them. Let’s take the following as an example.

Theorem. Let $X$ and $Y$ be sets. Then \((X \cap Y) \cup (X \setminus Y) = X\)

Here is another one.

Theorem. Let $X, Y$, and $Z$ be sets. Assume that $X \cap Y = \varnothing$. Then, \((X \times Z) \cap (Y \times Z) = \varnothing\)