Negation

In a debate or a courtroom, there are usually two opposing sides. One is arguing for $A$ and the other is arguing for not $A$.

In propositional logic, we introduce a symbol in the place of not: negation. It is denoted by $\neg$.

Given a formula $A$, then we can make a new one $\neg A$. But what should be the rules of inference that mimic our arguments involving not? When have I established not of a statement? What does knowing the negation of a statement allow me to conclude?

One common pattern is to start an argument with $A$ and reason until you reach something that is clearly not true. This leads us to also introduce a symbol $\bot$ which plays the role of false or “this is crazy”.

Then we can formalize our pattern of argument via the following introduction rule for $\neg$

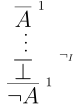
Given an argument assuming $A$ that leads to an absurdity, then we can conclude $\neg A$.

To eliminate $\neg$ we have

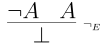
If both $\neg A$ and $A$ hold, then this is absurd.

What are the rules for introducing and eliminating $\bot$? We actually just saw the $\bot$-introduction above – it doubles as the $\neg$-elimination rule. The elimination rule is very general.

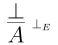
Once we have established $\bot$, then we are free to reach any conclusion.

Let’s do another example to see how our rules of deduction interact.

Example. Let’s establish $$\neg A \land \neg B \to \neg (A \lor B)$$

Recall this is shorthand for $\vdash (\neg A \land \neg B \to \neg(A \lor B))$. In words, this says we can establish $\neg A \land \neg B \to \neg (A \lor B)$ with no assumptions.

Proof. (Expand to view)

If we want to establish a conclusion of the form $X \to Y$ then we will want to introduce $\to$. To do that we need to provide a deduction of the form $$X \vdash Y$$ In our case, we want to fill in the details for $$\neg A \land \neg B \vdash \neg(A \lor B)$$ Now our goal is of the form $\neg Z$ so we want to introduce $\neg$. To do that, we need to supply a proof of $\bot$ from $Z$. We have reduced to establishing $$\neg A \land \neg B, A \lor B \vdash \bot$$ We could combine $A$ and $\neg A$, if we had them, to got $\bot$. The same holds for $B$ and $\neg B$. ee can eliminate $\neg A \land \neg B$ into either $\neg A$ or $\neg B$. For $A \lor B$ elimination, we need proofs of desired conclusion, here $\bot$, one with $A$ $$\neg A \land \neg B, A \vdash \bot$$ and one with $B$ $$\neg A \land \neg B, B \vdash \bot$$ The proofs of these are quicker.

Putting everything together, we get the following natural deduction proof. In step${}^0$, we cancel the assumption $\neg A \land \neg B$ to introduce $\to$. In step${}^1$, we cancel the assumption $A \lor B$ to introduce $\neg (A \lor B)$ since our conclusion is $\bot$. Finally the steps${}^2$, we cancel $A$ and $B$ using or elimination. The numerical labels are convenient to keep track of the cancellations. Note that all assumptions are cancelled. ■

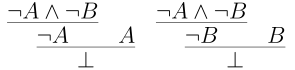
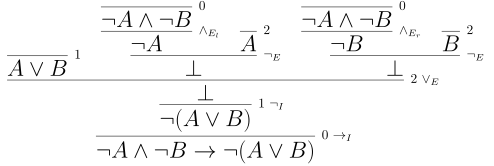
Ok so what is the value of this result? It gives a method of proof that holds no matter how we interpret $A$ and $B$.

For example, if we say $A$ is “it is hot out” and $B$ is “it is raining”, then we can interpret the above as saying “if I know that the either it is not hot out or it is not raining, then I can conclude that it is not both hot and sunny”.

Each of formula that we can prove symbolically is an argument pattern that can be applied in any context.

Some conventions

Expressions like $\neg \neg A$ are pretty un-ambiguous and we declare that $\neg$ binds most closely. So for example $$\neg A \to B := (\neg A) \to B \\ \neg C \lor D:= (\neg C) \lor D$$