Last time, we saw the beginnings of a formal system to represent logical reasoning. Here we introduce some operations on a collection of propositions to build expressions.

You can think of the propositions as the atoms of our system and the connectives we introduce as the bonds.

In addition, for each connective, we give a introductiona and elimination rule in deduction.

Conjunction

One basic rhetorical device is a take a bunch of statements and group them together with an and.

The murderer was cousin Mr. Plum and the weapon was the candlestick and the murder occured in the foyer.

The corresponding connective in logic has the fancy name of conjunction is denoted by $\land$. So if we have expressions $C$ and $D$, then $C \land D$ is another valid expression.

Now let’s think about what we can deduce assuming we know $C$ and $D$. It may seem silly but if we know $C \land D$ then we know $C$. So we have the following elimination rule for deduction

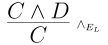
The notation we use for this move is $\land_{E_L}$.

Similarly, we have the right-sided analog.

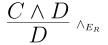
Then we have a introduction rule that mirrors: if we know that $C$ is true and $D$ is true, then we know that $C$ and $D$ is true.

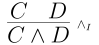
Note that at this level we know very little. For example, $A \land B \land C$ is ambigious. It is either \((A \land B) \land C\) or \(A \land (B \land C)\) But these are logically equivalent, meaning we can prove one from the other and vice-versa. Below we have \((A \land B) \land C \vdash A \land (B \land C)\)

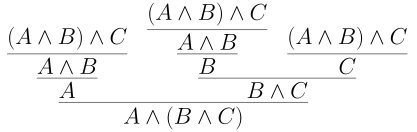
Can you give a proof for \(A \land (B \land C) \vdash (A \land B) \land C ~?\)

Disjunction

Another common rhetorical pattern is an argument by cases. Often the cases are exhaustive, like “it is sunny or it is not sunny”.

Our introduction rules are pretty straightforward.

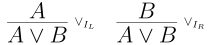
The elimination rule is a bit more subtle. If we want to reach our goal $C$ and we know that $A$ or $B$ is true, then we need to justify $C$ in two separate cases. One case for when $A$ is true and one case for when $B$ is true. This means that elimination needs to take in a proof $A \vdash C$ and $B \vdash C$.

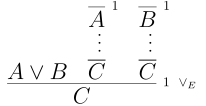
Note the lines above $A$ and $B$. This an example of hypothetical reasoning. We have assumed that $A$ is true and provided some argument to derive $C$. Similarly, we have assumed that $B$ is true and argued to $C$. Given both, then know that $A \lor B \vdash C$.

The superscipts ${}^1$ indicate where we introduce additional assumptions and where we cancel. The numbering helps up keep track of any hypotheses introduced.

Implication

Implication is basic step in a (natural language) logical argument. If we know that whenever $X$ is true, then so is $Y$. Then once we know that $X$ is true we get that $Y$ is also.

We have a connective symbol $\to$ for implication. Via our interpretation of proofs, one would likely also think of $X \vdash Y$ as type of implication. The introduction and elimination rules make this connection clearer.

First for elimination, we need to know $X \to Y$ and $X$ to conclude $Y$.

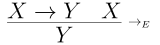
The introduction rule is

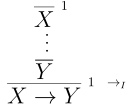
Bi-implication

Another connective is bi-implication, or commonly called iff for if and only if. It is denoted $\leftrightarrow$.

It has two elimination rules depending on whether we know $X$ or $Y$.

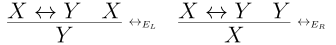
If we have a proofs $X \vdash Y$ and $Y \vdash X$ then we can conclude $X \leftrightarrow Y$.

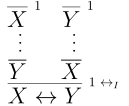
Let’s do an example proof to see how these rules interact.

Example. Let’s show that \((A \to B) \land (B \to C) \vdash A \to C\) So if $A$ implies and $B$ implies $C$, then $A$ implies $C$ if we intrepret it using words.

Proof. (Expand to view)

To prove $A \to C$, we want introduce a $\to$. This introduce says we can conclude $A \to C$ if we can establish $A \vdash C$. Thus, we can reduce to proving $$ (A \to B) \land (B \to C), A \vdash C $$ With $A$ and $A \to B$, we can eliminate to $B$. Then with $B$ and $B \to C$, we can eliminate to $C$. Below is a full proof.

■

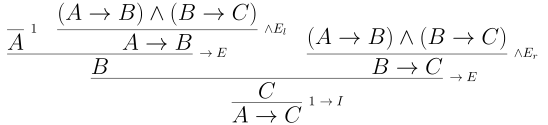
Here is another example.

Example. Let’s establish \(((A \lor B) \to C) \to ((A \to C) \land (B \to C))\)

Proof. (Expand to view)

Recall that $$ ((A \lor B) \to C) \to ((A \to C) \land (B \to C)) $$ is shorthand for $$ \vdash ((A \lor B) \to C) \to ((A \to C) \land (B \to C)) $$ In other words, we want to proof the formula without assumptions. We "backwards" similarly to the last example. To establish a goal of the form $X \to Y$, we need $X \vdash Y$. So it suffices to show $$ ((A \lor B) \to C) \vdash ((A \to C) \land (B \to C)) $$ Now to establish a goal with $\land$ we want to prove both sides of the $\land$. So we need two proofs $$ (A \lor B) \to C \vdash A \to C \\ (A \lor B) \to C \vdash B \to C $$ Again we can reverse the introduction rule for $\to$ to reduce to $$ (A \lor B) \to C, A \vdash C \\ (A \lor B) \to C, B \vdash C $$ We can use the introduction rules for $\lor$ to produce $A \lor B$ from either $A$ or $B$. Putting it all together we have

■

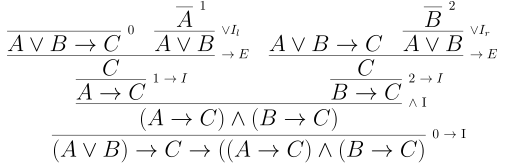
Some conventions

Writing out lots of $( \ )$ is tedious after awhile. We therefore establish some conventions on how to read a formula without paretheses.

First, all of $\to, \land,$ and $\lor$ associate right to left. This means that \(A \lor B \lor C := A \lor (B \lor C)\)

Then $\to$ binds more weakly that both $\lor$ and $\land$. For example \(A \lor B \to C \land D := (A \lor B) \to (C \land D)\)

It is important to remember that, in general, the placement of parentheses makes a difference!